There is saying, “If you cannot quantify it then ain’t worth anything in physics”.
It is has been this way since the time of Newton and Galileo who were the first to show the importance of expressing their ideas in mathematical terms. Thus prediction can be calculated and quantified in order to test their ideas by way of the experimental method.
“But what are the exact questions that I need to be asking?” Is the question that I continually ask myself such that I can formulate my hypothesis.
With the production of the “CPT Symmetry in a SuperVerse” episode I have managed to come very close to encapsulating my ideas in the context of a simple reproducible computational model. In order to create the visualisation of specific phenomena, like hypernova explosions, I made extensive use of the open-source 3D rendering software Blender and its physics engine.
One particular model, that I put together, managed to capture everything that I am trying to communicate in my work in a single cohesive model.
Reproduction of an experiment is one of the most important steps in the scientific method. Follow this Blender tutorial in order to build the model for yourself. You can download the Blender model file by clicking this link.
The model is simplicity itself and manages to capture the exact behaviour and mechanics of how a concentric ringed jet of vortices can arise under the influence of a single magnetic force field. At its base, it is a particle simulation. A particle simulation models the behaviour of many, usually thousands or millions of, particles under the influence of any number or type of force field.
The initial conditions for each particle is that their starting location is defined randomly within the volume of a sphere. In order for particles inside the Blender simulation to be able to interact with the magnetic force field they must have some initial momentum. If they have no momentum and instead are stationary they are unaffected by the magnetic force field and remain stationary. This is a constraint of Blender’s physics engine.
Animation of bipolar jet ejection using a point cloud density shader. You can download the Blender model file by clicking this link.
The initial particle’s direction of travel is outwards from the volume of the sphere. In essence, the particles represents that matter of the star that is exploding as it goes nova. In the first revision of this model, as linked to above, the particles are simply given an outward normal direction away from the sphere.
Thus if we run the model, without the presence of a magnetic force field, then all the particles move away from the sphere uniformly. That is, the particles collectively form a spherical ball shape that grows outwards at a constant rate equal to the particles’s initial speed.
Animation of model showing the emergence of the jet which bifurcates into a series of concentric ringed vortices. All arising from a single magnetic force field. You can download the Blender model file by clicking this link.
As a revision to this model I added a single point force field in the centre of the sphere that acts as the explosive force for the nova event. Thus rather than gradually move away from the sphere the particles rather explode out and away from the sphere.
Particle animation of model that focuses on the initial jet formation and the subsequent void that develops as the jet moves away. In this model we add an additional point force field to act as the explosive force of the supernovae event. This is particularly to demonstrate how a supervoid can develop at the end of the jet’s formation. You can download the Blender model file by clicking this link.
This is in comparison to an exploding star whose initial shape is defined as being the spherical volume occupied by the mass of the star that is about to go nova. The particles in the model therefore represent the mass of the star broken down into a series of random particles within its own volume. The initial velocity and direction of travel is analogous to the star exploding coming from the neutrino core-bounce event that actually physically rips the star apart.
The goal of the numerical model is to show the pattern of behaviour that arises from the soon to be defined magnetic field. Thus we attribute no information to the particles except to say they start within the volume of the exploding star. The core-bounce of neutrinos that causes the star to explode is given definition in our model by imparting a uniform outward trajectory to each particle.
Blender simulates particle physics by way of different “force fields” that are used to exert a force on each particle in order to govern its behaviour. There are a range of different force fields but in the context of our model we are only interested in defining a single magnet force field that is located at the north pole of our spherical volume.
The magnet force field is defined as a single point, at the north pole, with the axis of its poles running along the z-axis. It has a falloff defined as a sphere such that the influence of the magnetic field, upon the particles, decreases the further a particle is from the point where the field is located.
It should be noted that in the bipolar ejection model, where the blue jet is ejected from the north pole and the red jet is ejected from the south pole, that each of the two particle systems are influenced only by their pole’s respective magnet force field.
With the model defined we run, or rather bake, the simulation.
Particle animation of model that shows the individual particles as bubbles in a liquid medium. You can download the Blender model file by clicking this link.
In order to render the simulation I created a volumetric shader that uses a point cloud density shader. I found this to be a very computationally expensive process that can easily eat up the memory on your computer. If you find this to be the case I would recommend decreasing the number of particles in the simulation.
Alternatively, you may wish to simply render each particle and delete the volumetric shader. I have found that the point cloud density shader in Blender to be rather unreliable. By defining a simple icosphere with an emission shader you can assign this object to be rendered for each particle.
From the simulation we can see the particles start of as they explode out from the sphere. Under the influence of the magnetic force field, located at the north pole, they change direction. The majority of particles, following the open magnetic field lines, form the initial jet as a bulk. As the jet evolves we can see the first concentric vortices forming. Then we can see a second and a third.
The first, and what I think is the most important, detail is the shape of each of the concentric ringed vortices emerging from the bulk of the central jet. Namely, that they form a symmetrical cone shape with straight edges running from the apex to the emerging base.
The straight edge is extremely important because I need to be able to explain why we see a universe whose shape is mostly flat. Cosmologists for a long time have wondered what the shape of the universe is at the largest scales. Is it open, closed or flat?
By analysing the Cosmic Microwave Background Radiation it was discovered that the shape of the universe is indeed flat [1]. So in order for my Big Bang Hypernova Hypothesis to be valid I need to show why we have come to live in a universe that is mostly flat.
Since my earliest communication of what is now the Big Bang Hypernova Hypothesis I have been trying like mad to find the connection between vortices and the formation of straight sided cones. At first, I took a direct interpretation in considering the Lorentz light cone without really fully understanding and appreciating the purpose of the light cone in special relativity.
Another interpretation was in looking at the formation of vapour cones on aeroplanes travelling faster than the speed of sound. Here the shock wave, caused by the plane travelling at supersonic seeds, forms a shock c ollar where moisture in the air is suddenly compressed into a cloud. Looking at the formation of the shock collar we see a straight sided cone of vapour. But rather than the speed of sound being the constant measurement of velocity it is rather the speed of light.
The primary reason for looking at such a physical reaction first came from an observation regarding the finite difference method and the flow of information. My first observation of this comes from the book “Numerical Solution of Partial Differential Equations: Finite Difference Methods by G.D.Smith” [2]. Here the chapters are split into solutions for Parabolic equations; Hyperbolic equations and Elliptic equations.
Specifically, we define a general second order partial differential equation (PDE) as:
$$a(x_1,x_2)\frac{\partial^2u}{\partial x_1^2} + b(x_1,x_2)\frac{\partial^2u}{\partial x_1 \partial x_2} + c(x_1,x_2)\frac{\partial^2u}{\partial x_2^2} + d(x_1,x_2)\frac{\partial u}{\partial x_1} + e(x_1,x_2)\frac{\partial u}{\partial x_2} + f(x_1,x_2)u = g(x_1,x_2) \phantom{xxxxxxxxx}(1) $$Then the PDE, (1), is called elliptic when
$$b^2 - 4ac < 0\phantom{xxxxxxxxx}(2)$$The PDE, (1), is called parabolic when
$$b^2 - 4ac = 0\phantom{xxxxxxxxx}(3)$$And lastly, the PDE, (1), is called hyperbolic when
$$b^2 - 4ac > 0\phantom{xxxxxxxxx}(4)$$The Euler-Tricomi equation, (5), is used to describe the phenomenon of transonic flow:
$$\frac{\partial^2u}{\partial x^2} + x \frac{\partial^2u}{\partial y^2} = 0 \phantom{xxxxxxxxx} (5)$$Here the Euler-Tircomi equation is elliptic in the half plane where \(x>0\) It is hyperbolic in the opposite half plane, where \(x<0\) , and parabolic when \(x=0\).
It is this connection that really peaked my interest in thinking about vortices and the huge number of connections it has with physics. Firstly the phenomena of a straight lined cone, such as, the formation of a vapour cone. Then secondly, the significance that a specific speed limit is involved; in this specific case the speed of sound. Then thirdly, the difference in the flow of information and their associated computational algorithms in creating quantised and discrete numerical computer models employing the finite difference method.
In fact, one of the earliest models of the atom was a vortex model of the atom developed by William Thompson, later Lord Kelvin. This idea has seen a resurgence in popularity, particularly in light of quantum vortices and superfluids. And when it comes to thinking about pair annihilation and ringed vortices there is this fluid experiment.
In fact, quantum vortices played a star role in the popular show The Big Bang Theory as Sheldon and Leonard’s theory of everything. The actual specific area of physics is Superfluid Vacuum Theory and is a very good starting point in separating the contents of the Big Bang Hypernova from the surrounding vacuum as giving definition to what vacuum is in the SuperVerse.
But returning back to the straight edged concentric vortices of our particle simulation; this for me is a very important result. This is very important because it gives explanation to why we see a universe whose overall curvature is nearly flat as measured from the Cosmic Microwave Background Radiation [1].
Thus I am able to see the actual linkage between a universe that we measure as being flat, from the radiation of the Big Bang event itself, and my Big Bang Hypernova Hypothesis of our universe evolving as a concentric ringed series of vortices.
Namely, we see the straight edge of the cone as the outermost layer, of a given vortex ring, which forms coming from the diffusion of particles away from the axis of rotation defined by the poles of the magnetic force field.
The other factor is that the model itself forms a series of concentric ringed structures and this is the reason for the concentric circles as identified by Penrose upon the CMB [3].
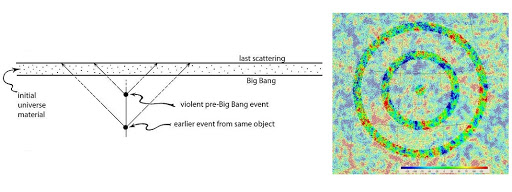
Example of a concentric ringed structure identified by Penrose on the CMB.
So here using a simple numerical model I can show the effects of a magnetic force field acting as a north pole upon a spherical volume of particles, as a simulation for jet formation. This jet formation shows two key features that have been identified and measured coming from the CMB. That is the flat measurement of the universe coupled with Penrose’s concentric circles in the CMB.
The second, and really important detail, in this simple numerical model is rotation. That is we can see rotation in the jet around the z-axis as defined by the poles of the magnetic field. From my point of view I see rotation in everything. From the smallest to the largest scale we can see rotation in everything.
In quantum mechanics all particles have the property of spin which is an intrinsic form of angular momentum or rotational momentum. The one exception to this is the Higgs boson, being the physical representation of the Higgs field, with a spin of zero. But this is because the Higgs field is in fact the central rotational axis around which everything else rotates. It is the central jet formation that runs along the z-axis in our numerical model.
Moving on up the scale, planets and stars rotate about their geographical polar axises giving rise to day and night here on Earth. The planets in our solar system orbit, or rather rotate, around the Sun. The passage of our solar system through the interstellar space of the Milky Way galaxy we see as rotating around the centre of the galactic core. Our sun, along with all the other stars in the Milky Way galaxy, orbits the galactic core and thus our galaxy has rotation.
Then on the largest scale we see that the entire universe appears to have a preferred rotation and direction. This is particularly in light of the non-isomorphic alignment of the lower dipoles of the CMB [4] and additionally and most recently in the preferred rotation of galaxies [5].
The third, and yet again really important detail, in this simple numerical model is symmetry. Now I have already given a very simple mathematical argument as to exactly how the pattern of a hypernova event can give rise to a CPT-symmetric universe and anti-verse. But it is only with this model that we begin to see the more complex details that it is closer to what I am ultimately trying to describe.
A circle and a ring are both infinitely symmetric. Thus the concentric vortex rings that make up our reality are also infinitely symmetric.
The importance of symmetry to physics [6] was really given form in Noether’s theorem. Her theorem implicitly showed the fundamental link between conservation laws and symmetry. Gauge theory, from quantum mechanics, again also places symmetry front and centre. Then of course there is the case for observing a reality, where through rigorous experimentation, we see a CPT-symmetric universe.
In fact many physicists consider CPT-symmetry to be a fundamental law of physics. However I would argue it is not. As I’ve already argued, we can see the underlying reason for why we live in a CPT-symmetric universe has come about arising from the initial conditions that is the Big Bang Hypernova event.
In order to test my ideas about the superfluidity of the universe in combination with trying to break CPT-symmetry I came straight down on the Martin Tajmar’s work [7]. The ability to do local frame dragging, without the need for exotic matter, using rotating liquid helium [8] is what I currently consider to be probably the single most important experiment in all of history.
Why has this experiment not been reproduced? Most likely it is because it breaks the hallowed CPT-symmetry by extending the magnetic field out to become a quasi-gravitational force.
But this particular video brought the work of Ning Li and Eugene Podkletnov to my attention.
Really, it is Ning Li who I would really credit now as being the real pioneer [9] in this work with her work regarding gravity [10] and superconductors [11]. Ning Li, setup her own company, in order to pursue this line of research but has never published any results. However it is being funded from the US Department of Defence and is still in existence. I guess they have found something and this is probably now the most highly guarded secret in the US military, outside the S4 site at Area 51.
Then there is the work of Russian scientist Eugene Podkletnov using superconductors with composite crystal structure [12]. This was taken seriously enough that Boeing developed Project Grasp which if I understand right is still ongoing, receiving US DoD grants, even though people have become very quiet about it.
I’ll be blunt! If I was given a grant I would not be using it on telescope observation I’d be trying to reproduce Martin Tajmar’s work. I know the tip end of the warp drive when I see it.
But when it comes to gravity I do not think we know the whole story yet. This is particularly in light of trying to properly unpack the proposition of my new axiomatic rule:
Gravity is equivalent to the electromagnetic force, but on the next scale up in the SuperVerse.
For instance consider, Coulomb’s Law which calculates the force between two charged particles:
$$ F=k_e \frac{q_1 q_2}{r^2} \phantom{xxxxxxxxx} (6) $$Then we consider Newton’s Law of Universal Gravitation which calculates the gravitational attractive force between two bodies with mass:
$$ F=G\frac{m_1m_2}{r^2} \phantom{xxxxxxxxx} (7) $$
- Both equations calculate the force exerted between two bodies.
- Both equations are inverse-distance squared proportionality laws.
- Both equations are proportional based on a defined constant.
Remember, fractal geometry is the cosmological principle. Thus self-similar patterns repeat themselves irrespective of scale.
Here we see the same pattern in the equations of (6) and (7). Thus we can make the logical conclusion that the electrostatic force is equivalent to the gravitational force, but on the next scale up.
But the electric force is only half the picture of the total force. Namely, there is the magnet force as well which is one and the same as it is the electromagnetic force. An electromagnetic wave has two components: Firstly there is the electric wave and secondly there is the magnetic wave which runs perpendicular to it.
We know gravity forms waves and with the detection by LIGO we have confirmed their theoretical existence. So logically there must be a perpendicular component to a gravitational wave. A “gravo-magnetic” component for use of a better term.
Then there is the fact that it is a magnetic force field that gives actual shape to our particle simulation in Blender. It is not an electric force field. It is a magnetic force field that is employed to give shape to the concentric series of vortices. So that means my entire hypothesis, in terms of this computational model, is reliant on the existence of this new “gravo-magnetic” field.
What exactly that means and what kind of experiment or observation could be used to prove such a concept? Is the question! In presenting this computational model and showing how it accounts for identified features in the CMB radiation is one step along the path to answering that question.
Another step along that path is in trying to imagine what the ultimate computational model presenting the Big Bang Hypernova Hypothesis would look like. Such a model should account for the formation of galaxies. So let us try and imagine the formation of galaxies where at the heart of each galaxy there lives a supermassive black hole that were the seeds of galaxy formation.
Supermassive black holes, as I’ve argued, were born from the ultimate act of fusion as the core of the MacLean collapsed in on itself. These were in turn blown out from the MacLean as each of the twin jet-a-verses were born. This is the process we can see at the start of the model. But being the heaviest particles in the jet they were the first to be swung to form the outer ring because of the centrifugal force arising from the rotation around the central axis.
Now a key argument I have presented is that the rules of quantum mechanics came into being because of the initial conditions of the Big Bang. That being that a MacLean went hypernova. The actual force that shaped our jet-a-verse was gravity following the proposition of my new axiomatic rule:
Gravity is equivalent to the electromagnetic force, but on the next scale up in the SuperVerse.
Or rather it was shaped more by a gravo-magnetic force from our previous discussion.
The importance of the computational model is that it produces a pattern of behaviour, arising from the influence of a single magnetic force field, that accounts for two key features identified by cosmologists on the Cosmic Microwave Background Radiation. Specifically, a flat microwave sky [1] and Penrose’s concentric circles [3]. In future essays we will see how this model, and our new axiomatic rule unpacks, as it accounts for the CMB Cold Spot; the unusual anisotropic alignment in the lower dipoles of the CMB [4]; coupled with dark flow and The Great Attractor.
In the “CPT Symmetry in a SuperVerse” episode we saw how the pattern of a hypernova can give rise to a CPT-Symmetric universe. Following the work of Andrei Sakharov's 2D didactic model who showed that a twin cosmological model was a direct consequence of the laws of quantum mechanics and CPT symmetry. Further to this we have both cosmologists Julian Barbour and Jean-Pierre Petit work which proves, via General Relativity, that it was gravity and not quantum mechanics that shaped our universe. We shall also explore, in future essays, how solutions of General Relativity via Maximally Extended Penrose Diagrams explicitly show a parallel universe. Moreover we finally give name to the collapsed core of the MacLean; a white hole.
In contrast, the Lambda-CDM model was an idealistic model. It was idealistic because it saw the laws of quantum mechanics as immutable. Meaning the same laws of physics as they are here on Earth were the same at the time of the Big Bang. Thus experiments, such as those at the LHC and Fermilab, could reproduce the conditions of the Big Bang. Hence we could test ideas by the experimental method. Unfortunately, it looks like this is not the case; particularly in light of this study [13] showing variation in alpha, the fine-structure constant.
Unlike the Lambda-CDM model however the Big Bang Hypernova Hypothesis is only beginning to develop its own language and grammar. I mean only a page ago we invented, or discovered, a new concept; namely the “gravo-magnetic” field. So we don’t have sufficient description in order to convey the birth process that led to the laws of quantum mechanics as we measure them here on Earth.
In place of this we will employ the language that has developed around the Lambda-CDM model and the Big Bang theory as it currently stands. So for instance, the initial mass of the jet before it bifurcates into concentric layers is best described as a quark-gluon plasma. But it is very important to bear in mind that quarks, and their respective fields, arise from the initial jet in the context of the Big Bang Hypernova Hypothesis. The laws of quantum mechanics emerge from the initial conditions of the Big Bang and did not exist before the hypernova of the MacLean.
With this all said, let me describe how I imagine the final evolution of a computational model. Specifically a model that accounts for the formation of active galaxies in the very early universe.
So we imagine two major components that form the initial bulk of the jet. The first component is the quark-gluon plasma. The second component is the ejection of the supermassive black holes out with the jet.
From the point of view of our original particle simulation we can imagine the particles as being the supermassive black holes themselves. As gravity already exists as a force in its own right being a component of the SuperVerse then it means matter is attracted towards it. Or rather the quark-gluon plasma that surrounds the black holes is drawn in towards it because of its gravitational attractive force.
The distribution of the quark-gluon plasma throughout the initial formation of the jet could be considered to be fairly homogenous. In essence the outward matter being ejected is being swept up in the ultimate liquid blender in the hypernova of the MacLean. So as milk mixes with tea when stirred so to is our quark-gluon plasma being stirred. Also by extension so are the supermassive black holes being fairly homogeneously distributed throughout the initial formation of the jet. We can see such a distribution in our particle simulation.
Another attribute we impart to the supermassive black holes is that they have rotation. In many ways I see supermassive black holes as being the particles of the SuperVerse. Particles have spin and so to do supermassive black holes. Certainly a key feature is that we can say the MacLean had rotation. Probably impossibly fast rotation, faster than light rotation I would venture to conjecture. I say this particularly in light of Philipp Mosta’s supercomputer simulations of hypernovae which require a fast spinning star [14].
So even if the supermassive black holes did not have rotation when fused together they soon had rotation. This rotation would be imparted to them by the surrounding medium being in rotation.
With this said, we imagine the evolution of the jet. As the supermassive black hole particles travel through the quark-gluon plasma this matter is dragged along with it. It is not only dragged but also starts to rotates. For the exact same reason and mechanics as a star being born forms an accession disc of dust and gas because of gravity so too does our supermassive black holes form accretion discs. Thus our mostly homogenous quark-gluon plasma mixture is separated into forming accretion discs around the supermassive black hole particles.
And then the black hole begins to feed and the active galaxy is born.
Or rather it is a proto-active galaxy. The laws of quantum mechanics is only just now emerging in the vacuum spaces in the separating jets. As quarks becomes protons and neutrons which in turn bind to electrons in order to form hydrogen. And only once hydrogen exists then can stars in the galaxies form.
But this creation of an accretion disc first is what gave shape to our galaxies. Or more specifically it explains how and why half the galaxies are spiral galaxies. It also goes to explain how and why we see so many active quasar galaxies in the far off distant and early universe.
References:
- [1] A Flat Universe from High-Resolution Maps of the Cosmic Microwave Background Radiation : P. de Bernardis, P.A.R.Ade, J.J.Bock, J.R.Bond, J.Borrill, A.Boscaleri, K.Coble, B.P.Crill, G.De Gasperis, P.C.Farese, P.G.Ferreira11, K.Ganga, M.Giacometti, E.Hivon, V.V.Hristov, A.Iacoangeli, A.H.Jaffe, A.E.Lange, L.Martinis, S.Masi1, P.Mason, P.D.Mauskopf, A.Melchiorri, L.Miglio, T.Montroy, C.B.Netterfield, E.Pascale, F.Piacentini, D.Pogosyan, S.Prunet, S.Rao, G.Romeo, J.E.Ruhl, F.Scaramuzzi, D.Sforna, N.Vittorio
- [2] Numerical Solution of Partial Differential Equations: Finite Difference Methods by G.D.Smith
- [3] Concentric circles in WMAP data may provide evidence of violent pre-Big-Bang activity. V. G. Gurzadyan and R. Penrose
- [4] The significance of the largest scale CMB fluctuations in WMAP. Angelica de Oliveira-Costa, Max Tegmark, Matias Zaldarriaga & Andrew Hamilton
- [5] Multipole alignment in the large-scale distribution of spin direction of spiral galaxies. Lior Shamir
- [6] The role of symmetry in fundamental physics. David J. Gross
- [7] Search for Frame-Dragging-Like Signals Close to Spinning Superconductors. M. Tajmar, F. Plesescu, B. Seifert, R. Schnitzer, and I. Vasiljevich
- [8] Evaluation of enhanced frame-dragging in the vicinity of a rotating niobium superconductor, liquid helium and a helium superfluid. M Tajmar
- [9] Gravitational effects on the magnetic attenuation of superconductors. Ning Li and D. G. Torr
- [10] Gravitoelectric-electric coupling via superconductivity. Douglas G. Torr & Ning Li
- [11] Effects of a gravitomagnetic field on pure superconductors. Ning Li and D. G. Torr
- [12] Impulse Gravity Generator Based on Charged \(Y Ba_2 Cu_3 O_{7-y}\) Superconductor with Composite Crystal Structure. Evgeny Podkletnov, Giovanni Modanese
- [13] Probing variation of the fine-structure constant using the strong gravitational lensing. L.R.Colac, R.F.L.Holanda and R.Silva
- [14] A large scale dynamo and magnetoturbulence in rapidly rotating core-collapse supernovae. Philipp Mösta, Christian D. Ott, David Radice, Luke F. Roberts, Erik Schnetter, & Roland Haas